|
RENTREE TERRESTRE ARC ATMOSPHERIQUE |
![]()
|
CONTENU : Mis
à jour décembre 2005, revu sept 2011 2°) Calculs intermédiaires de la mise en équations 1°) Premier groupe d'équations 2°) Deuxième groupe d'équations 3°) Cas particulier d'une rentrée équatoriale NB
: le téléchargement regroupe 4 cours sur la rentrée Rentrée d'Allen - Rentrée de Chapman - Déorbitation Arc atmosphérique |
|
![]()
Ce
cours sur l'arc atmosphérique de la rentrée est le troisième volet sur la
rentrée et en termine l'étude :Le premier étudiant la manœuvre
de déorbitation, le
deuxième étant l'étude le l'arc orbital de descente, les 2 permettant de
"régler" les conditions de rentrée dans l'atmosphère d'une planète.
Nous
nous intéressons tout particulièrement à la Terre, mais les calculs seront
aisément adaptables à Mars par exemple.
La
mise en équations est un peu complexe et demande de la précision. Par souci
pédagogique, nous donnons les fondements des calculs, les difficultés
principales et laisserons le lecteur intéressé, réaliser lui même les
développements intermédiaires.
L'étude
engagée doit permettre de calculer à chaque instant, la trajectoire d'une
capsule de rentrée, dans le repère de Greenwich, afin de bien maîtriser le
point de chute au sol.
De
manière très générale, le problème du mouvement d'un point en 3 dimensions,
demande 6 équations, 3 portant sur la dérivée du rayon vecteur et 3 sur la
dérivée du vecteur vitesse qui n'est autre que la loi fondamentale de la
dynamique.

Nous
prenons donc 6 paramètres, mais plus adaptés au problème du suivi de la capsule
par des moyens au sol :
Coordonnées géographiques de positionnement :
L la longitude Greenwich
l
la latitude géocentrique équatoriale
r la norme du rayon vecteur
Paramètres de repérage du vecteur vitesse :
V norme du vecteur vitesse de la capsule par rapport à l'atmosphère
g
la pente du vecteur vitesse relative, angle entre le plan horizontal local et
le vecteur vitesse, compté >0 si le vecteur vitesse est au dessus de ce plan
b
l'azimut relatif qui, on le rappelle mesuré positivement vers l'Est.
2°) REPERES ET CALCULS
INTERMEDIAIRES :
a)
Repère absolu Ro:
La
loi fondamentale de la dynamique nécessite un repère inertiel, nous prendrons
donc OIJK, le géocentrique équatorial, associé au système J2000.
b)
Repère relatif R de repérage du mouvement du véhicule:
Pour
un mouvement rapporté à la Terre, nous choisirons comme repère relatif,
parfaitement adapté, R le repère de Greenwich qui tourne ainsi que
l'atmosphère, à vitesse angulaire constante wT par
rapport à Ro.
La
loi fondamentale se présente alors sous la forme particulière faisant
intervenir les forces dites d'inertie d'entraînement et de Coriolis:

c)
Autres repères ou axes intermédiaires :
La
figure suivante concerne l'aérodynamique:

a) REPERE AERODYNAMIQUE XYZ= REPERE DE CALCUL R1:
On nomme ainsi le repère X Y W intimement lié à la vitesse air et aux forces
aérodynamiques:

NB
: Les équations du mouvement du véhicule de rentrée seront projetées sur les axes
X Y W de ce repère noté R1
b)
INCIDENCE : Le véhicule de rentrée, avec son axe longitudinal i, dont
l'angle avec le vecteur vitesse s'appelle l'incidence i.
Ici,
l'incidence est >0, fournissant donc une portance vers le haut, c'est le
"vol sur le ventre", permettant de limiter le taux de descente et de
rester en altitude. Dans le cas contraire, avec i<0 et donc un "vol sur
le dos", la portance est vers le bas et la trajectoire s'incline plus vers
le bas, augmentant le taux de descente.
c) ANGLE DE GITE : Cet angle définit la rotation du
véhicule, à INCIDENCE CONSTANTE, autour de l'axe X ou encore du vecteur
vitesse. Sur la figure, la GITE est positive, assurant une portance inclinée du
côté droit du véhicule quand on le regarde de face.
EXEMPLE
: Pour un angle de gite de 90° ou de - 90° le véhicule est "sur la
tranche".
Cet
angle est, plus que l'incidence, un paramètre essentiel d'une stratégie de
pilotage et de guidage du véhicule vers un point de chute visé.
d)
FORCES AERODYNAMIQUES :Donnons immédiatement l'expression de la force
aérodynamique, avec sa décomposition en traînée RX et portance Rz:

La
dépendance par rapport au nombre de Mach, des coefficients aérodynamiques de
traînée et de portance n'apparaît qu'en subsonique, car en hypersonique, il
sont pratiquement constants.
e)
REPERE ENZ : une figure plus haut( celle avec la Terre ) montre le repère
géographique local ENZ, avec E l'Est, N le nord local et Z la verticale
ascendante. Le dessin montre aussi clairement le vecteur u unitaire de la
projection de la vitesse sur le plan horizontal. Ce vecteur u intervient dans
la définition de l'azimut b et de la
pente g.
1°)
CELLES CONCERNANT L, l, r :
Sans
grosse difficulté la vitesse de l'extrémité de Z , vue du repère de Greenwich,
ne dépend que des rotations L et l.
donc:

Nous obtenons ainsi un premier groupe d'équations:

2°)
CALCULS INTERMEDIAIRES CONCERNANT V, b, g :
Nous
traduisons alors la loi fondamentale, en projection sur les axes du repère
aérodynamique XYW, avec comme vraies forces, la traînée, la portance et le
poids. Nous détaillons ci-dessous les calculs intermédiaires.
a)
Accélération de Coriolis sur XYW:

Tout
simplifié, on a sur XYW:

b)
Accélération d'entraînement sur XYW :
Des
calculs analogues, moins détaillés, vus les précédents, donnent :

c) Accélération relative exprimée sur X Y W :
Le
calcul repose sur 3 idées
1-
Que l'accélération relative se calcule comme si la terre était fixe
2-
D'une dérivation en axes relatifs, utilisant au passage ENZ
3-
Que X dans ENZ ne dépend que des angles b
et g.

Le
lecteur achèvera les calculs analogues aux précédents, qui donnent :

et
grâce aux dérivées connues de la longitude et de la latitude, il vient :

3°)
EQUATIONS CONCERNANT V, b, g :
En explicitant la loi fondamentale, il vient le
deuxième groupe d'équations où G est l'accélération due à la gravitation et non
le poids, avec Rx et Rz qui ont les expressions vues plus haut.
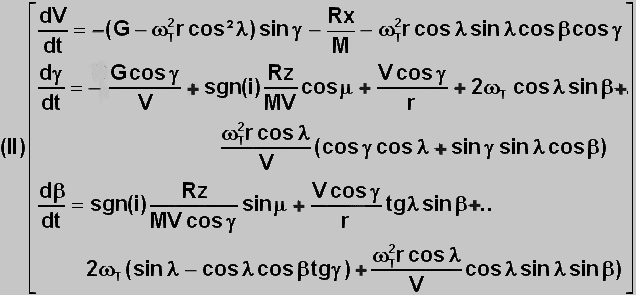
4°)
CONCLUSIONS :
Le
système des équations (I) et (II) constitue l'ensemble des équations à
résoudre.
En
posant un nouveau vecteur Y de l'espace vectoriel R6, il vient le
système fermé :

qui
se résout numériquement, par un algorithme d'intégration, par exemple
Runge-Kutta ordre 4, avec la donnée des conditions initiales.
NB :
Le lecteur aura bien compris que g est la
pente relative, donc en général négative, pour une rentrée atmosphérique, du
moins dans les premiers instants de la rentrée. Il est clair qu'éventuellement
cet angle peut momentanément devenir positif lors de "rebonds" sur
les couches denses de l'atmosphère; une évasion est même possible après
rebond..
Probablement
un projet de rentrée utilisera ces équations.
Si
l'on considère une rentrée équatoriale, dans le sens de la rotation terrestre,
c'est à dire vers l'Est, les équations se simplifient grâce à :
l
= 0, b = 90°, m = 0 (
pas de gite pour éviter un déport latéral).

Des
projets de rentrée ou de vol lanceur ( en ajoutant la poussée) utiliseront ces
équations un peu plus simples.
III QUELQUES IDEES SUR LE GUIDAGE :
Indiquons
que, pour une capsule spatiale classique de forme conique, qui n'est pas une
navette, la capacité à créer une portance est limitée, ou ce qui est équivalent
la finesse ( quotient de la portance par la traînée ou encore Cz/Cx) maximum
est faible. Nous dirons que les capsules ont du mal à planer.
Il
est clair que des erreurs inévitables se produisent sur les conditions de
rentrée, longitude, latitude, ...., angle, vitesse, que la modélisation de
l'atmosphère ne peut être parfaite et qu'une activité solaire subite peut
notablement modifier localement la densité atmosphérique, etc...
Ces
considérations conduisent donc à la mise en place d'une stratégie, permettant
de rejoindre au mieux un point cible, tout en respectant certaines limitations
de décélération maximale ou de température du bouclier thermique. C'est la
NOTION DE NAVIGATION-GUIDAGE-PLILOTAGE, encore dénommée NGP.
1°)
GUIDAGE EN GITE ET ROULIS :
Ce
type de guidage a été mis en œuvre lors des premiers retours, depuis des
orbites circumterrestres, des premiers vols habités.
Le
point de chute est choisi sensiblement à mi-distance des points de chute à
finesse nulle ( rentrée balistique) et du point de chute en utilisant tout au
long de la rentrée la portance maximale.
a)
La rentrée commence avec une attitude donnant la finesse et donc la portance
maximum.
POURQUOI?
Tout simplement pour ne pas arriver trop tôt et donc trop vite dans les couches
atmosphériques denses autour de 40 à 60 km d'altitude. On limite donc la
décélération maximale.
Il faut
par exemple savoir qu'à finesse nulle, une rentrée balistique à partir d'une
orbite circulaire basse, à angle quasiment nul conduit à une décélération
maximale de 8.3 g, et pour un angle de 6°, un pic de 16 g
La
prise de portance abaisse notablement le niveau maximum de la décélération et
permet de rester en dessous de 4.5 g.
b)
On attend d'intercepter une trajectoire de descente à finesse nulle, qui
conduit au point cible. Pour annuler la portance, le véhicule est mis en roulis
de façon à créer une portance de valeur moyenne nulle.
c)
Il est clair que cette stratégie a "oublié" le guidage latéral. Donc
de temps en temps le roulis est stoppé et le guidage latéral assuré par la
prise d'une GITE à 90° ou - 90°, qui respecte donc la finesse verticale nulle(
pas de portance dans le plan vertical) et permet par le signe de la gite un
déport latéral à gauche ou à droite grâce à la portance horizontale.
Le
dessin suivant illustre le propos.

VARIANTE --> LE GUIDAGE MOITIE PORTANT:
Les
américains ont aussi utilisé, en quelques occasions, une trajectoire dite à
MOITIE PORTANTE. En clair, la capsule adopte, une incidence donnant la portance
maximum et une attitude en gite ( m =
60°, donc cosm = 0.5 =) qui permet d'avoir une
finesse moitié de la finesse max.
Il
reste donc, en jouant sur la gite m,
une capacité de pilotage, par exemple :
Si
le point cible trop loin, ne peut être atteinte à portance moitié, il faut faire
"planer" un peu plus, donc prendre une plus grande portance, on
diminue la gite et le tour est joué.
Voir
les équations en V et g où intervient cosm, surtout celle en g.
Réciproquement
si la trajectoire moitié portante, risque de dépasser la cible, il faut
"plonger" un peu plus vers le sol, on "casse" la pente en
diminuant la portance, donc on augmente la gite.
Le
prix à payer est un déport latéral à maîtriser, en jouant sur le signe de la
gite, ce qui ne change rien à la portance, mais joue sur la composante latérale
et donc en particulier sur l'azimut ( rôle de sinm dans l'équation en c ).
2°)
GUIDAGE EN FINESSE :
Pour
les véhicules de rentrée modernes, comme la Navette US, plus loin la capsule
Apollo, l'aérodynamique du véhicule et les capacités de pilotage permettent
d'utiliser une finesse précise.
a)
On commence à simuler la rentrée du véhicule, avec un modèle élaboré
d'atmosphère et un pilotage moyen à incidence fixée. Les calculs informatiques
fournissent donc une trajectoire de référence Co, sur laquelle on est capable
de tabuler:
La
"FINESSE VERTICALE fv", en fonction de la vitesse relative
V.

L'altitude
Zo(V) en fonction de la vitesse V, autant dire le profil d'altitude fonction de
la vitesse.
b)
Durant la rentrée réelle, soumise à des perturbations et à des dispersions des
paramètres de rentrée, le véhicule garde une incidence fixe, et les moyens
inertiels de mesure à bord, permettent de mesurer V la position du véhicule en
axes Greenwich et donc d'évaluer l'écart en altitude Z(V) - Zo(V).
c)
Le guidage est réalisé par un asservissement de la finesse verticale de type
PID sur le profil de référence, de la forme:
 00
00
avec
des gains K1, K2, K3 positifs à choisir et à optimiser.
d)
Comment alors réaliser physiquement la finesse théorique fv, à incidence
constante?
En
jouant sur l'angle de gite m qui devient
la COMMANDE, ce qui laisse une possibilité de contrôle du déport latéral, par
le signe de cet angle.
![]()
f
la finesse réelle est simplement définie par l'incidence fixe adoptée et le
nombre de Mach instantané.
IV DONNEES NUMERIQUES SUR L'ATMOSPHERE TERRESTRE :
Tirées du site : http://www.braeunig.us/space/atmos.htm#si
|
Physical Properties of
Standard Atmosphere in SI Units |
||||
|
Altitude |
Temperature |
Pressure |
Density |
Viscosity |
|
|
||||
|
-5000 |
320.7 |
1.778E+5 |
1.931 |
1.942E-5 |
|
-4000 |
314.2 |
1.596E+5 |
1.770 |
1.912E-5 |
|
-3000 |
307.7 |
1.430E+5 |
1.619 |
1.882E-5 |
|
-2000 |
301.2 |
1.278E+5 |
1.478 |
1.852E-5 |
|
-1000 |
294.7 |
1.139E+5 |
1.347 |
1.821E-5 |
|
0 |
288.2 |
1.013E+5 |
1.225 |
1.789E-5 |
|
1000 |
281.7 |
8.988E+4 |
1.112 |
1.758E-5 |
|
2000 |
275.2 |
7.950E+4 |
1.007 |
1.726E-5 |
|
3000 |
268.7 |
7.012E+4 |
9.093E-1 |
1.694E-5 |
|
4000 |
262.2 |
6.166E+4 |
8.194E-1 |
1.661E-5 |
|
5000 |
255.7 |
5.405E+4 |
7.364E-1 |
1.628E-5 |
|
6000 |
249.2 |
4.722E+4 |
6.601E-1 |
1.595E-5 |
|
7000 |
242.7 |
4.111E+4 |
5.900E-1 |
1.561E-5 |
|
8000 |
236.2 |
3.565E+4 |
5.258E-1 |
1.527E-5 |
|
9000 |
229.7 |
3.080E+4 |
4.671E-1 |
1.493E-5 |
|
10000 |
223.3 |
2.650E+4 |
4.135E-1 |
1.458E-5 |
|
15000 |
216.7 |
1.211E+4 |
1.948E-1 |
1.422E-5 |
|
20000 |
216.7 |
5.529E+3 |
8.891E-2 |
1.422E-5 |
|
30000 |
226.5 |
1.197E+3 |
1.841E-2 |
1.475E-5 |
|
40000 |
250.4 |
2.871E+2 |
3.996E-3 |
1.601E-5 |
|
50000 |
270.7 |
7.978E+1 |
1.027E-3 |
1.704E-5 |
|
60000 |
255.8 |
2.246E+1 |
3.059E-4 |
1.629E-5 |
|
70000 |
219.7 |
5.520 |
8.754E-5 |
1.438E-5 |
|
80000 |
180.7 |
1.037 |
1.999E-5 |
1.216E-5 |
|
90000 |
180.7 |
1.644E-1 |
3.170E-6 |
1.216E-5 |
![]()
Guiziou Robert janvier 2002-
complété novembre 2004, corrigé décembre 2005, sept 2011